 |
| Charles-Augustin de Coulomb |
Ley de Coulomb Teoría:
La ley de que la fuerza entre cargas eléctricas es inversamente proporcional al cuadrado de la distancia entre las cargas fue demostrada experimentalmente por el químico británico Joseph Priestley alrededor de 1766. Priestley también demostró que una carga eléctrica se distribuye uniformemente sobre la superficie de una esfera metálica hueca, y que en el interior de una esfera así no existen cargas ni campos eléctricos. Charles de Coulomb inventó una balanza de torsión para medir con precisión la fuerza que se ejerce entre las cargas eléctricas. Con ese aparato confirmó las observaciones de Priestley y demostró que la fuerza entre dos cargas también es proporcional al producto de las cargas individuales. La fuerza entre dos partículas con cargas q1 y q2 puede calcularse a partir de la Ley de Coulomb:
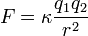
en donde q y q' corresponden a los valores de las cargas que interaccionan tomadas con su signo positivo o negativo, r representa la distancia que las separa supuestas concentradas cada una de ellas en un punto y K es la constante de proporcionalidad correspondiente que depende del medio en que se hallen dichas cargas.
(1) Donde:
F: fuerza de atracción o repulsión entre las cargas, Newton
q1; q2: carga eléctrica de la partícula, Coulomb
r12: distancia más corta entre las dos cargas, metros
constante de permitividad eléctrica del medio en el cual se encuentran inmersa las cargas, 
La constante de permitividad eléctrica del vacío es 8,85 x 10-12  ; recuérdese que 1 Coulomb es equivalente a 1 ampere.segundo. En el caso de realizar análisis en distribución continua de carga, se utilizará la siguiente expresión:
; recuérdese que 1 Coulomb es equivalente a 1 ampere.segundo. En el caso de realizar análisis en distribución continua de carga, se utilizará la siguiente expresión:
(2) Cuando se conoce la densidad de carga del elemento de , se emplea:
(3) Donde:
dq: diferencial de carga, Coulomb
dx: diferencial de longitud, m
Si es una superficie lo que se estudia, se emplea:
(4) Donde:
dq: diferencial de carga, Coulomb
dA: diferencial de área, m2
Si es un volumen lo que se analiza, se emplea:
(5) Donde:
dq: diferencial de carga, Coulomb
dV: diferencial de , m3
Por último, es de vital importancia conocer las siguientes constantes y conversiones:
- Masa de un electrón: 9,11 x 10-28 g
- Carga de un electrón: 1,6 x 10-19 Coul
- Masa de un protón: 1,67 x 10-24 g
- Diámetro de un átomo: 2 x 10-8 cm (promedio)
- Un Coulomb equivale a 6 x 1018 electrones
- Un Coulomb equivale a 3 x 109 Statcoulomb
Se debe tener presente que la electricidad sólo reside en la superficie de los objetos cargados, no en su interior.
Permitividad relativa de algunas substancias:
Substancias gggr
Vacío 1
Aire (seco, sin CO2) 1,0005
Agua (a 20 ºC) 80,1
Vidrio para ventanas 7,0
Madera 2 - 8
Aplicaciones Ley Coulomb:
1 - Intensidad de campo eléctrico originada por unadistribución discreta de cargas puntuales o equivalentes.
2 - Fuerza que ejerce una distribución discreta de cargas sobre otra carga.
Ley de Coulomb, Ejemplo de su Aplicación
Suponga que se tiene tres cargas puntuales localizadas en los vértices de un triángulo recto, como se muestra en la figura, donde q1 = -80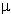 C, q2 = 50
C, q2 = 50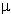 C y q3 = 70
C y q3 = 70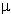 C, distancia AC = 30 cm, distancia AB = 40 cm. Calcular la fuerza sobre la carga q3debida a las cargas q1 y q2.
C, distancia AC = 30 cm, distancia AB = 40 cm. Calcular la fuerza sobre la carga q3debida a las cargas q1 y q2.
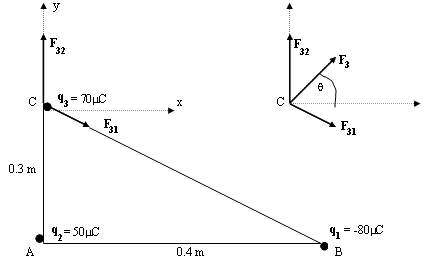
Las direcciones de las fuerzas sabemos coinciden con las líneas que unen a cada par de cargas puntuales. La fuerza que q1 ejerce sobre q3, F31, es de atracción. La fuerza que q2 ejerce sobre q3, F32, es de repulsión. Así, las fuerzas F31 y F32 tienen las direcciones que se indican. La separación entre q3 y q1 se obtiene de (CB)2 = (AC)2 + (AB)2 = (0.3 m)2 + (0.4 m)2, de donde CB = 0.5 m.
Las magnitudes de tales fuerzas son:
F31 = [(9x109 Nm2 /C2)(80x10-6 C)(70x10-6 C)]/ (0.5 m)2
= 201.6 N
F32 = [(9x109 Nm2 /C2)(5 0x10-6 C)(70x10-6 C)]/ (0.3 m)2
= 350 N
Conviene disponer ejes coordenados xy tal como se indica en la figura, con el origen en la carga donde deseamos calcular la fuerza resultante, en este caso en q3.
Llamando F3 a la fuerza resultante sobre q3, entonces F3
= F31 + F32 . Luego, en términos de componentes x e y :
F3x = F31x + F32x
F3y = F31y + F32y
F31x = F31cos = (201.6 N)x(40/50) = 161.3 N ; F31y
= (201.6 N)x(40/50) = 161.3 N ; F31y
= - F31sen = -201.6x30/50 = -121 N
= -201.6x30/50 = -121 N
F32x = 0 ; F32y = F32 = 350 N
F3x = 161.3 N + 0 = 161.3 N ; F3y = -121 N + 350 N = 229 N
La magnitud de la fuerza neta F3 se obtiene de (F3)2
= (F3x)2 + (F3y>)2, resultando F3 = 280 N. El ángulo de esta fuerza se obtiene de tg = F3y/ F3x= 229/161.3
= F3y/ F3x= 229/161.3
= 1.42 ==>  = 54.8º.
= 54.8º.
Aplicaciones de la Ley de Coulomb
Ejemplo 1.
Esferas en contacto.
Dos esferas A y B están en el vacío separadas por una distancia de 10 cm. Tienen cargas eléctricas de qa= +3x10-6C y qb= - 8x10-6C. Una esfera C en estado neutro, primero toca a la esfera A y después a B. Si la esfera C después de tocar a B se separa del sistema, Calcular la fuerza con que se accionan las cargas de Ay B.
La fuerza eléctrica es más de 1039 veces mayor que la fuerza gravitacional. En otras palabras, las fuerzas eléctricas que se ejercen entre las partículas atómicas son tan superiores a las fuerzas gravitacionales que éstas pueden ser totalmente despreciadas.
Ejercicios Ley De Coulomb:
Ejercicio C-1 Determinar la fuerza que actúa sobre las cargas eléctricas q1 = + 1 x 10-6 C. y q2 = + 2,5 x 10-6 C. que se encuentran en reposo y en el vacío a una distancia de 5 cm. |  |
Resolución:
Para calcular la fuerza de interacción entre dos cargas eléctricas puntuales en reposo recurriremos a la ley de Coulomb por lo tanto previo transformar todas las magnitudes en juego a unidades del sistema internacional de medidas nos queda que:
Como la respuesta obtenida es de signo positivo nos está indicando que la fuerza es de repulsión.
Respuesta:
La fuerza de repulsión tiene un módulo de 9 N. pero debemos indicar además en un esquema gráfico las demás características del vector tal como se indica en el gráfico.

Ejercicio C-2 Determinar la fuerza que actúa sobre las cargas eléctricas q1 = -1,25 x 10-9 C. y q2 = +2 x 10-5 C. que se encuentran en reposo y en el vacío a una distancia de 10 cm. |  |
Resolución: Para calcular la fuerza de interacción entre dos cargas eléctricas puntuales en reposo recurriremos a la ley de Coulomb por lo tanto previo transformar todas las magnitudes en juego a unidades del sistema internacional de medidas nos queda que: Como la respuesta obtenida es de signo negativo nos está indicando que la fuerza es de atracción. Respuesta: La fuerza de atracción tiene un módulo de 2,25 x 10-2 N. pero debemos indicar además en un esquema gráfico las demás características del vector lo que sería así:  |
La siguiente figura muestra tres partículas cargadas:
¿Qué fuerza electrostática, debida a las otras dos cargas, actúa sobre q1?
Considere que:
q1= -1.2 μC
q2= 3.7 μC
q3= -2.7 μC
r12= 15 cm
r13= 10 cm
θ= 32°
Recordemos que μ (micro) significa 10 elevado a la menos 6
o sea que -1.2 μC es igual a -1.2x10^-6 C
Por la Ley de Coulomb sabemos que la fuerza que va a ejercer la carga q2 sobre q1 es igual a:
F12= K (q1q2)/(r12)²
donde la constante k= 9x10⁹ Nm²/C²
F12= 1.776 N
Ahora calculamos la fuerza que ejerce la carga q3 sobre la carga q1:
F13= K(q1q3)/r13
F13= 2.484 N
Nota: Al realizar los cálculos de la fuerza, no tomamos en cuenta el signo de las cargas, ya que por ahora sólo nos interesa la magnitud de dicha fuerza.
Ahora vamos a descomponer los vectores obtenidos (F12 y F13) en sus correspondientes componentes rectangulares:
La componente en x de F12 es igual a la magnitud de la fuerza que obtuvimos anteriormente, es decir Fx12= 1.77 N
Y la componente F13x= F13 sen 32°
Fx= Fx12 + Fx13= 3.09 N
Ahora obtenemos las componentes en Y:
Fy= F12y + F 13y
La componente en y de F12= 0
Fy= 0 + (-F13 cos 32°)
Fy= -2.10 N
la fuerza resulta negativa porque la carga q1 y q3 tienen el mismo signo
por lo tanto se repelen.
La fuerza total ejercida por las cargas q2 y q3 sobre q1 se obtiene:
F= √(3.09²)+(- 2.10²)
F= 3.74 N
Considere que:
q1= -1.2 μC
q2= 3.7 μC
q3= -2.7 μC
r12= 15 cm
r13= 10 cm
θ= 32°
Recordemos que μ (micro) significa 10 elevado a la menos 6
o sea que -1.2 μC es igual a -1.2x10^-6 C
Por la Ley de Coulomb sabemos que la fuerza que va a ejercer la carga q2 sobre q1 es igual a:
F12= K (q1q2)/(r12)²
donde la constante k= 9x10⁹ Nm²/C²
F12= 1.776 N
Ahora calculamos la fuerza que ejerce la carga q3 sobre la carga q1:
F13= K(q1q3)/r13
F13= 2.484 N
Nota: Al realizar los cálculos de la fuerza, no tomamos en cuenta el signo de las cargas, ya que por ahora sólo nos interesa la magnitud de dicha fuerza.
Ahora vamos a descomponer los vectores obtenidos (F12 y F13) en sus correspondientes componentes rectangulares:
La componente en x de F12 es igual a la magnitud de la fuerza que obtuvimos anteriormente, es decir Fx12= 1.77 N
Y la componente F13x= F13 sen 32°
Fx= Fx12 + Fx13= 3.09 N
Ahora obtenemos las componentes en Y:
Fy= F12y + F 13y
La componente en y de F12= 0
Fy= 0 + (-F13 cos 32°)
Fy= -2.10 N
la fuerza resulta negativa porque la carga q1 y q3 tienen el mismo signo
por lo tanto se repelen.
La fuerza total ejercida por las cargas q2 y q3 sobre q1 se obtiene:
F= √(3.09²)+(- 2.10²)
F= 3.74 N
Algunos Vídeos e Imágenes Para Poder Comprender La Ley De Coulomb:
Ley De Coulomb





